Minimization of DFA in Hindi (Minimization of Automata Machines)

Unit 2

Types of Finite Automata

Topic 4 : Minimization of DFA in hindi (Minimization of Automata Machines)

Automata theory (Theory Computer की एक Branch) में, DFA Minimization एक दिए गए Deterministic Finite Automaton (DFA) (DFA) को एक समान DFA में बदलने का कार्य है जिसमें States की Minimizationसंख्या होती है। यहां दो DFA को समान कहा जाता है यदि वे एक ही Regular Language को पहचानते हैं। इस कार्य को पूरा करने वाले कई अलग-अलग algorithm Automata theory पर standard textbooks में known और described हैं

प्रत्येक Regular Language के लिए, एक minimal automaton भी मौजूद होता है जो इसे Accept करता है, अर्थात, एक DFA जिसमें Minimum Number में State होते हैं और यह DFA Unique होता है | Minimum DFA pattern matching जैसे कार्यों के लिए Minimum computational लागत सुनिश्चित करता है।

States के दो वर्ग हैं जिन्हें Language को प्रभावित किए बिना मूल DFA से Removedया Merged किया जा सकता है, इसे कम से कम करना स्वीकार करता है।

Unreachable states वे State हैं जो किसी input String के लिए DFA की initial state से उपलब्ध नहीं हैं।
Nondistinguishable state वे होते हैं जिन्हें किसी भी input string के लिए एक दूसरे से अलग नहीं किया जा सकता है।

DFA minimization आमतौर पर 3 Step में किया जाता है, relevant States को Removed या merged करने के लिए। चूंकि nondistinguishable States का Elimination computational रूप से सबसे महंगा है, इसलिए इसे आमतौर पर last step के रूप में किया जाता है।

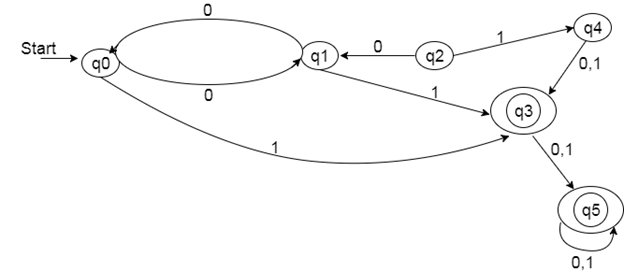
Minimization of DFA in hindi (Minimization of Automata Machines)

Solution:

Step 1 : दिए गए DFA में, q2 और q4 unreachable states हैं, इसलिए उन्हें Remove कर दें।

Step 2 : बाकी States के लिए transition table बनाएं।

State

→q0

*q3

*q5

Step 3 : अब transition table की rows को दो sets में divide करें

1. एक set में वे rows होती हैं, जो non-final states से शुरू होती हैं

State

2. एक other set में वे rows होती हैं, जो Final State से शुरू होती हैं।

State	0	1
q3	q5	q5
q5	q5	q5

Step 4: Set 1 में समान rows नहीं हैं, इसलिए set 1 समान होगा।

Step 5: Set 2 में, row 1 और row 2 q3 और q5 के समान है क्योंकि 0 और 1. एक ही state में transit करते हैं और इसलिए q5 को छोड़ दें और फिर बाकी में q5 को skip करें।

State	0	1
q3	q3	q3

Step 6: अब Set 1 को set करें और 2 को set करें

State	0	1
→q0	q1	q3
q1	q0	q3
*q3	q3	q3

NP Complete Problem in Hindi

NP-Complete problems एक महत्वपूर्ण वर्ग हैं जो computational complexity the...

Multihead Turing Machine और Multidimensional Turing Machine की विशेषताएँ और अंतर

Multihead Turing Machine एक प्रकार की Turing Machine है जिसमें एक से अ�...

Universal Turing Machine and Multitape in Hindi

Universal Turing Machine (UTM) एक ऐसी ट्यूरिंग मशीन है, जो किसी भ...

Techniques for Turing Machine Construction in Hindi

Turing Machine कंप्यूटर विज्ञान में एक theoretical model है, जो क�...

Petri Net Model in Hindi | Theory of Computation (TOC) Explained

Petri Net एक mathematical model है जो systems के behavior को graphically represent करने �...

Minimization of DFA in Hindi (Minimization of Automata Machines)